Machine Design February 1993

New vibration isolators perform ten times better than air springs

DAVID L. PIATUS
Minus K Technology Inc., Los Angeles, Calif.

Laser Interferometer Vibration Isolation
Negative-stiffness-mechanism isolators offer unsurpassed vibration control
In the 2 to 100-Hz range.

Vibration is a fact of life in most industrial settings, but in some applications it cannot be tolerated. When fabricating microelectronics, machining to extreme tolerances, or using industrial laser/optical systems, for example, a vibration-free environment is a must.

Until recently, air springs offered the best vibration isolation. But newly developed negative-stiffness mechanism (NSM) isolators control 2 to 100-Hz vibrations 10 to 100 times better than air springs.

Vertical and horizontal isolators combined in a single package provide a passive, mechanical 6-DGF (degrees of freedom) isolator. They are suitable for fixed static loads, applications where load changes are small, and those where adjustments for load changes can be made. Among the benefits the devices bring to a manufacturing environment are:

Better resolution and accuracy from inspection instruments.
Higher yield from fabrication equipment because of fewer rejects or rework.
Greater versatility in locating vibration sensitive equipment, such as on upper floors of a building instead of the basement.

When compared to air springs, NSM isolators:

Require no air or power supply.
Have no valves to maintain or replace.
Do not generate heat.
Cannot contaminate clean rooms with dirty air.
Offer natural-frequency adjustment independent of load.
Are all metal; they can be used in hard vacuums, at high temperatures, and in radiation environments.
Used its passive elements in active systems, give faster response to load changes and can automatically adjust natural-frequency.
Negative-stiffness isolators use mechanical components to keep vibrations from sensitive equipment.

The net result is a compact isolator capable of low vertical and horizontal stiffnesses and high internal structural frequencies.

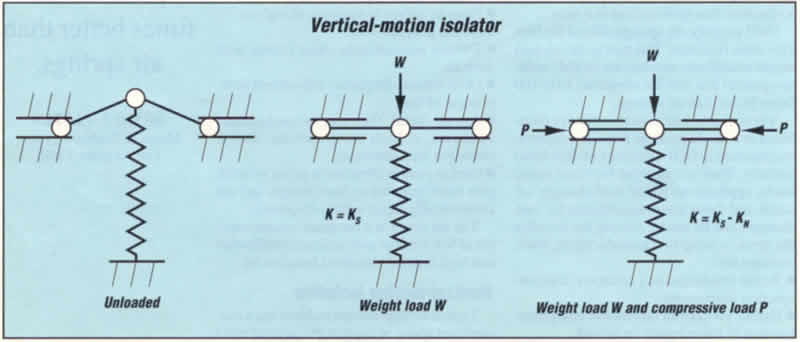
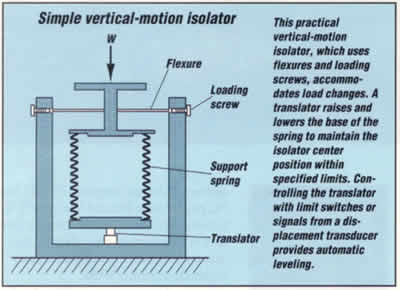
Vertical-motion isolation
Typical vertical-motion isolators use a conventional spring to support the pay load and a negative-stiffness mechanism ("snap-through" or "over-center" mechanism) to cancel some or all of the spring stiffness. This produces low to zero net vertical stiffness. The approach has been used successfully to simulate zero gravity when testing large space structures, for example, but has not been previously used in 6-DOF isolation systems.

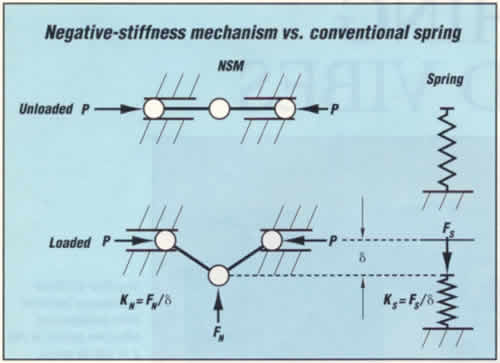One form of NSM consists of two bars hinged at the center, supported at their outer ends on pivots which are free to move horizontally, and loaded in compression by opposing forces P, When unloaded, the bars are aligned and in unstable equilibrium {the center position of the NSM.) When displaced downward an amount , force FN which opposes the motion holds the center hinge in equilibrium. For small values of , the ratio between FN and is linear and expressed as the negative stiffness, KN. The behavior of a conventional spring is also shown, both unloaded and deflected an amount by the force FS. Here, FS acts in the direction of the displacement to hold the deflected spring in equilibrium. The ratio of FN to is the positive stiffness KS.

Combining the spring and NSM produces a vertical-motion isolator. When a load W deflects the spring to the center position of the isolator, the spring provides vertical stiffness. Applying forces P to the bars creates the NSM, which cancels some or all of the spring stiffness. The resulting isolator stiffness is K= KS-KN, and can be made to approach zero while the spring still supports the weight. Flexures used in place of hinged bars offer advantages in some systems. Loading screws, piezoelectric devices, and various other means produce compressive loads.

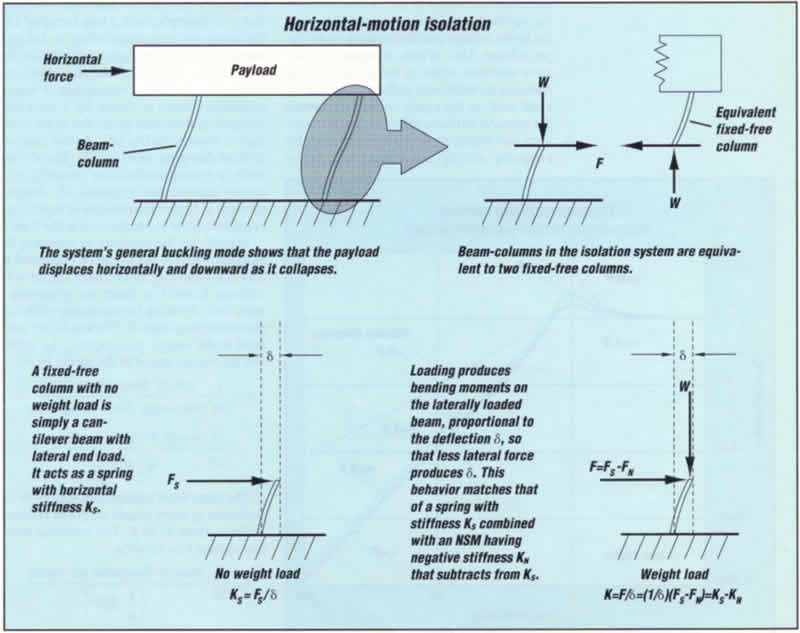
Horizontal-motion isolation
A set of flexible columns or beam-columns that behave as springs, combined with NSMs, isolate horizontal motion. This is illustrated by a payload supported on two flexible columns. A horizontal force displaces the payload without significant rotation because the columns are much stiffer vertically than horizontally. Horizontal stiffness can approach zero by loading the columns near their critical buckling loads, thereby producing very low natural frequencies for horizontal vibrations.

The system's general buckling mode is illustrated by a deformed shape. As the system collapses the payload moves horizontally and downward. Adding stops to limit horizontal displacement produces a system that is fail-safe against collapse due to inadvertent overload. Limiting horizontal displacements to small values changes the buckling mode and increases the buckling strength nominally by a factor of four Of course, the system does not isolate when the payload hits the stops.

This approach uses the beam-column effect: axial loading reduces bending stiffness of a beam-column. The beam-columns in the isolation system shown are equivalent to two fixed-free columns. For a single fixed-free column with no load weight, the beam-column is simply a cantilever beam with lateral (horizontal) end load, and acts as a spring with horizontal stiffness KS. Load W produces bending moments on the laterally loaded beam, proportional to the deflection , so that less lateral force produces . This behavior matches that of a spring with stiffness KS combined with an NSM having negative stiffness KN that subtracts from KS. As W approaches the critical buckling load. KN approaches KS and the net horizontal stiffness of the beam-column approaches zero.

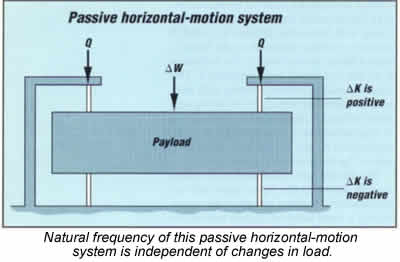
The simple horizontal-motion isolation system shown in the figure passively accommodates changing weights while maintaining a fixed isolation-system natural frequency. Two sets of flexible columns preloaded with axial load Q support the payload. Each set has an upper and lower column. The lower column supports part of the weight plus the axial preload; the upper column supports only the axial preload.

Because of the columns' axial flexibility and other flexibility in the system, increasing payload weight increases axial load on the lower column and decreases it on the upper column. This, in turn, increases the negative-stiffness effect in the lower column, reducing its horizontal stiffness. Decreasing axial load on the upper column decreases the negative stillness effect in the upper column, increasing its horizontal stiffness. By properly sizing the upper and lower columns, the horizontal stiffness changes in proportion to changes in payload weight, so the natural frequency remains unchanged.

Changing the preload Q changes the negative-stiffness effect in the upper and lower columns in the same direction, thereby providing an independent means for adjusting the system horizontal stiffness and resonant frequency.

Damping
Damping limits resonant responses. Reducing stiffness with the NSM magnifies the inherent system damping, resulting in high hysteretic damping. High hysteretic damping is more desirable than high viscous damping because it limits resonant responses without significantly reducing isolation efficiencies at higher frequencies.

Transmissibility curves shown for a hysteretically damped system illustrate this fact. For example, with a loss factor of 1.0, the resonant transmissibility is 1.4 and transmissibilities at higher frequencies deviate only slightly from the ideal undamped curve. For comparison, a transmissibility curve is shown for a viscously damped system that gives the same resonant transmissibility of 1.4 (the viscous critical-damping ratio is 0.5). The difference in transmissibilities between viscously damped and hysteretically damped systems at higher frequencies is significant considering the log scale used in the figure.

Magnifying the damping by reducing the stiffness with the NSM can be explained as follows. Consider an ordinary spring with stiffness KS and loss factor S, supporting a mass and vibrating harmonically with displacement amplitude . The loss factor is related to the energy dissipated in the spring and the energy stored in the spring by

The same basic relationship applies to the isolation system where an NSM reduces stillness from KS to K. The resulting isolation system loss factor is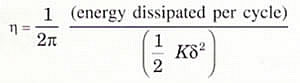 as the NSM reduces net stiffness K, the maximum elastic energy stored during the cycle, and associated with , decreases, but the energy dissipated per cycle does not, The energy dissipated per cycle is the energy dissipated by the spring, and can be expressed by the first equation. Combining the two equations gives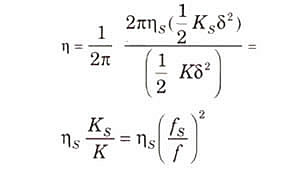where S is system natural frequency based on the spring stiffness and is system natural frequency based on the reduced stiffness.

The system's general buckling mode is illustrated by a deformed shape. As the system collapses the payload moves horizontally and downward. Adding stops to limit horizontal displacement produces a system that is fail-safe against collapse due to inadvertent overload. Limiting horizontal displacements to small values changes the buckling mode and increases the buckling strength nominally by a factor of four Of course, the system does not isolate when the payload hits the stops.

This approach uses the beam-column effect: axial loading reduces bending stiffness of a beam-column. The beam-columns in the isolation system shown are equivalent to two fixed-free columns. For a single fixed-free column with no load weight, the beam-column is simply a cantilever beam with lateral (horizontal) end load, and acts as a spring with horizontal stiffness KS. Load W produces bending moments on the laterally loaded beam, proportional to the deflection , so that less lateral force produces . This behavior matches that of a spring with stiffness KS combined with an NSM having negative stiffness KN that subtracts from KS. As W approaches the critical buckling load. KN approaches KS and the net horizontal stiffness of the beam-column approaches zero

Damping can be greatly magnified in a typical NSM isolation system. For example, consider a vertical-motion isolation system, where the spring's frequency is 5 Hz, and the NSM's is 0.5 Hz. According to the third equation, the isolation system loss factor equals the spring loss factor multiplied by 100. Therefore, 1% structural damping in the spring produces 100% structural damping in the isolation system.

Adding damping improves the suspension system, particularly high-damping viscoelastic materials. Consider a suspension consisting of a steel spring and viscoelastic damper. The system stiffness is the sum of the spring and damper stiffnesses, but essentially all the damping comes from the viscoelastic material. By adding negative stiffness with an NSM equal to the stiffness of the steel spring, the resulting suspension behaves dynamically as though the payload were suspended on only the damper. This approach produces very low natural frequencies and high damping in compact systems.

The damping behavior of viscoelastic materials typically falls between the viscous and the hysteretic curves shown in the transmissibility graph. Loss factors for some materials exceed 1.0 over certain ranges of temperature and frequency, and manufacturers can tailor materials to particular ranges of interest. For example, some materials have loss factors exceeding 1.0 at room temperature and the low frequencies of interest for vibration isolation -0.2 lo 1.5 Hz. Thus, system resonant transmissibilities lower than 1.4, and transmissibilities at the higher frequencies close to ideal undamped systems, are possible.

System stiffness can be reduced below that of the damping material alone, producing system resonant transmissibilities significantly lower than 1.4. However under these conditions in totally passive systems, creep instability can occur. By retaining some positive stiffness from the mechanical suspension, the system is inherently stable.

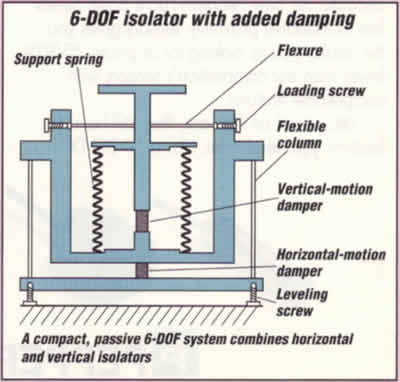SYSTEM CONFIGURATIONS
Isolators for handling vertical and horizontal vibrations can be combined to produce various configurations of 6-DOF isolators.

Passive systems
Compact, passive 6-OOF isolators with added damping are available with height and width approximately equal. Size envelopes for this configuration are comparable to pneumatic isolators that support the same loads. Other isolators depart radically from conventional shapes, including low-profile configurations for use where space is limited.

NSM suspensions arc applicable for a wide range of loads. For example, a small isolated platform that supports a microscope and a large system that support an entire fabrication-room floor can both give very low frequencies.

Active and automatic leveling systems
An important feature of NSM systems is their capability for stiffness and frequency control by adjusting the NSMs. For example, vertical and horizontal-motion isolators can be combined with a servosystem. Controlling the vertical-motion translator produces an automatic leveling system in which the horizontal-motion natural frequency is insensitive to changes in payload weight. Likewise, controlling the vertical-motion NSM makes vertical-motion natural frequency insensitive to weight changes. As another example, consider step-and-repeat systems, such as photolithography machines, with stages that accelerate and decelerate. Feed-forward control can adjust the NSMs to stiffen the system during stage acceleration and deceleration and soften the system during exposures or measurements.

Real-world systems
NSM isolation system behavior closely approaches the transmissibility curves up to frequencies where the isolator structure itself resonates. Because the isolators are simple, compact, elastic structures, their internal-structural resonances arc readily predictable and can be kept at high frequencies. Isolator resonances are above 100 Hz in practical 6-DOF systems with isolation system natural frequencies (frequencies at which the system of payload and suspension resonates) of 0.2 Hz or lower.

System natural frequencies in the range of 0.5 to 1.5 Hz are of interest for a wide range of applications, particularly with low system resonant response, near-hysteretic damping behavior and isolator internal-structural resonances above 100 Hz. With high-damping viscoelastic materials, resonant transmissibilities as low as 1.4 are practical with passive NSM-isolation systems. Automatic centering systems using an actuator controlled by signals from displacement or velocity sensors further enhance performance. Also, because NSM isolators are simple elastic structures and viscoelastic materials that deform, their isolation performance does not degrade with micromotions typical of laboratory floors and fabrication rooms, as with conventional pneumatic isolators.

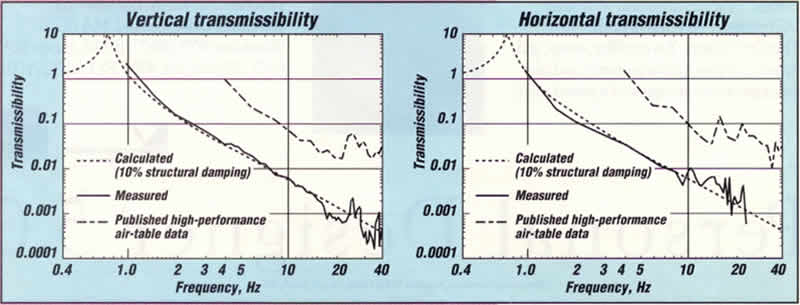
GAUGING PERFORMANCE
NSM-isolator performance between a system's natural frequency and first internal structural frequency closely approaches that of a perfect single-DOF system. Commercially available models have internal structural frequencies above 100 Hz.

Measured transmissibility versus frequency curves for a payload supported on three NSM isolators are shown in the figures. Calculated curves for single-DOF systems are shown for comparison, as are transmissibility curves for a high-performance air table, based on manufacturer's published data.

The measured curves are truncated at the upper frequencies by signal-to-noise ratios and at the lower frequencies by transducer frequency-responses.

PDF version of this article

Top